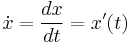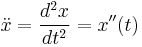Newton's notation
Newton's notation for differentiation, or dot notation, uses a dot placed over a function name to denote the time derivative of that function. Newton referred to this as a fluxion.
Isaac Newton's notation is mainly used in mechanics. It is defined as:
and so on.
Dot notation is not very useful for higher-order derivatives, but in mechanics and other engineering fields, the use of higher than second-order derivatives is limited.
Newton did not develop a standard mathematical notation for integration but used many different notations; however, the widely adopted notation is Leibniz's notation for integration.
In physics, macroeconomics and other fields, Newton's notation is used mostly for time derivatives, as opposed to slope or position derivatives.